Testwiki:অনুবাদ/আৰ্কিমিডিছ

আৰ্কিমিডিছ নামে অসমীয়া ৱিকিপিডিয়াত সন্নিবিষ্ট পোখালি প্ৰবন্ধটোত তলৰ কথাখিনি অনুবাদ কৰি শেষ হোৱাৰ পাছত সংযোগ কৰি দিয়ে যেন|

আৰ্কিমিডিছ (গ্ৰিক বৰ্ণমালা) আৰ্খিম্যাদ্যাস্‌, (গ্ৰিক ভাষা)বা সিৰাকাসেৰ আৰ্কিমিডিছ (খ্ৰি.পূ. ২৮৭-২১২) এজন [গণিত|গণিতবিদ][পদাৰ্থবিজ্ঞান|পদাৰ্থবিজ্ঞানী], [প্ৰকৌশল|প্ৰকৌশলী], [জ্যোতিৰ্বিদ্যা|জ্যোতিৰ্বিদ]] দাৰ্শনিক। যদিও তেখেতৰ জীৱন সম্পৰ্কে খুব কমই জানা গেছে, তবুও তেঁওক ক্ল্যাসিক্যাল যুগেৰ অন্যতম সেৰা বিজ্ঞানী হিচাপে বিবেচনা কৰা হয়। পদাৰ্থবিদ্যায় তেখেতৰ উল্লেখযোগ্য অবদানেৰ মাজত ৰৈছে স্থিতিবিদ্যা আৰ প্ৰবাহী স্থিতিবিদ্যাৰ ভিত্তি স্থাপন আৰু লিভাৰেৰ কাৰ্যনীতিৰ বিস্তাৰিত ব্যাখ্যাপ্ৰদান। পানি তোলাৰ বাবে আৰ্কিমিডিছৰ স্ক্ৰু পাম্প, যুদ্ধকালীন আক্ৰমণেৰ বাবে [সীজ siege সীঝ়্‌) ইঞ্জিন ইত্যাদি মৌলিক যন্ত্ৰপাতিৰ ডিজাইনেৰ বাবেও তেওঁ বিখ্যাত। আধুনিক বৈজ্ঞানিক পৰীক্ষায় তেখেতৰ নকশাকৃত আক্ৰমণকাৰী জাহাজকে পানি পৰা তুলে ফেলাৰ যন্ত্ৰ বা পাশাপাশি ৰাখা একগুচ্ছ আয়নাৰ সহায়ে জাহাজে অগ্নিসংযোগেৰ পদ্ধতি সফলভাবে বাস্তবায়ন কৰা সম্ভব হৈছে।

আৰ্কিমিডিছকে সাধাৰণত প্ৰাচীন যুগেৰ সেৰা আৰু সৰ্বাকালেৰ অন্যতম সেৰা গণিতজ্ঞ হিচাপে বিবেচনা কৰা হয়। তেওঁ মেথড অফ এক্সহশন ব্যবহাৰ কৰে অসীম ধাৰাৰ সমষ্টিৰূপে প্যাৰাবোলাৰ বক্ৰৰেখাৰ অন্তগৰ্ত ক্ষেত্ৰেৰ ক্ষেত্ৰফল নিৰ্ণয় কৰে আৰু পাই -এৰ প্ৰায় নিখুঁত এটা মান নিৰ্নয় কৰে। ইয়াৰ বাদেওও তেওঁ আৰ্কিমিডিছৰ স্পাইৰালেৰ সংজ্ঞা দেন, বক্ৰতলেৰ ক্ষেত্ৰফল নিৰ্ণয়েৰ সূত্ৰ প্ৰদান কৰে আৰু অনেক বড় সংখ্যাকে সহজে প্ৰকাশ কৰাৰ এটা চমৎকাৰ পদ্ধতি আবিষ্কাৰ কৰে।

যদিও ৰোমানৰা আৰ্কিমিডিছৰ কোন ক্ষতি কৰাৰ উপৰ নিষেধাজ্ঞা ছিল, কিন্তু ৰোমানদেৰ সিৰাকিউজ অবৰোধেৰ সময় এক ৰোমান সৈন্যেৰ হাতেই আৰ্কিমিডিছ নিহত হন। ৰোমান দাৰ্শনিক সিসেৰো আৰ্কিমিডিছৰ সমাধীৰ উপৰে এটা সিলিণ্ডাৰেৰ ভেতৰে আবদ্ধ এটা গোলকেৰ উল্লেখ কৰিছে। আৰ্কিমিডিছ প্ৰমাণ কৰেআছিল যে সিলিণ্ডাৰেৰ ভেতৰ আবদ্ধ গোলকটিৰ আয়তন আৰু ভূমিৰ ক্ষেত্ৰফল উভয়ই সিলিণ্ডাৰেৰ দুই তৃতীয়াংশ, যা আৰ্কিমিডিছৰ সেৰা গাণিতিক অৰ্জনসমূহৰৰ এটা হিচাপে বিবেচিত।

প্ৰাচীনকালে আৰ্কিমিডিছৰ গাণিতিক ৰচনাগুলি তেখেতৰ উদ্ভাবনসমূহৰৰ মত পৰিচিত ছিল না। আলেকজান্দ্ৰিয়াৰ গণিতবিদৰা তেখেতৰ লেখা পড়েছেন, বিভিন্ন জায়গায় উল্লেখও কৰিছে, কিন্তু আনুমানিক ৫৩০ খৃষ্টাব্দে গ্ৰিক স্থপতি ইসেডোৰ অফ মিলেতাস সৰ্বপ্ৰথম তেখেতৰ সকল ৰচনা একত্ৰে লিপিবদ্ধ কৰে। পৰৱৰ্তীতে ষষ্ঠ শতাব্দীতে গ্ৰিক গণিতবিদ ইউতোশিয়াস আৰ্কিমিডিছৰ কাজেৰ উপৰ এটা বিবৰণ প্ৰকাশ কৰে, যা তেঁওক প্ৰথমবাৰেৰ মত বৃহত্তৰ পাঠকসমাজেৰ কাষত পৰিচিত কৰে তোলে। আৰ্কিমিডিছৰ কাজেৰ খুব কম লিখিত দলিল মধ্যযুগেৰ পৰ অবশিষ্ট ছিল। কিন্তু সেই অল্পকিছু দলিলই পৰৱৰ্তীতে ৰেনেসাঁ যুগেৰ বিজ্ঞানীদেৰ কাষত খুগ্ৰন্থ উপকাৰী বলে বিবেচিত হয়। ১৯০৬ চনত আৰ্কিমিডিছৰ এটা নতুন পাণ্ডুলিপি আবিষ্কৃত হয় যা তেখেতৰ গাণিতিক সমস্যা সমাধানেৰ পদ্ধতিৰ উপৰ নতুনভাবে আলোকপাত কৰে।

জীৱনী

ব্ৰোঞ্জনিৰ্মিত আৰ্কিমিডিছৰ এই মূৰ্তিটি বাৰ্লিনেৰ আৰ্কেনহোল্ড অবজাৰভেটৰিতে অবস্থিত। এৰ ভাস্কৰ গেৰহাৰ্ড থীয়েম আৰু এটি ১৯৭২ চনত উন্মোচন কৰা হয়।

আৰ্কিমিডিছ আনুমানিক ২৮৭ খৃষ্টপূৰ্বাব্দে তৎকালীন বৃহত্তৰ গ্ৰিসেৰ উপনিবেশ সিসিলি দ্বীপেৰ সিৰাকিউজ নামেৰ বন্দৰ নগৰীতে জন্মগ্ৰহণ কৰে। বাইজান্টাইন গ্ৰিক ঐতিহাসিক জন যেতজেসেৰ বিবৰণ অনুযায়ী আৰ্কিমিডিছ পঁচাত্তৰ বছৰ বয়সে মাৰা যান, সেখান পৰা তেখেতৰ জন্মসাল সম্পৰ্কে ধাৰণা কৰা হয়। দ্য স্যাণ্ড ৰেকোনাৰ নামক দলিলে আৰ্কিমিডিছ তেখেতৰ বাবাৰ নাম ফিডিয়াস বলে উল্লেখ কৰে। ফিডিয়াস এজন জ্যোতিৰ্বিদ আছিল, যাঁৰ সম্পৰ্কে আৰ কিছু জানা সম্ভব হয়নি। ঐতিহাসিক প্লুটাৰ্খ তেখেতৰ দ্য প্যাৰালাল লাইভস নামক জীৱনী গ্ৰন্থে আৰ্কিমিডিছকে সিৰাকিউজেৰ ৰাজা দ্বিতীয় হিয়েৰোৰ আত্মীয় বলে উল্লেখ কৰে। আৰ্কিমিডিছৰ বন্ধু হেৰাক্লিডিস তেখেতৰ এটা জীৱনী লিখেআছিল, কিন্তু সেটি পৰৱৰ্তীতে হাৰিয়ে যায়। আৰ্কিমিডিছৰ জীৱনেৰ অনেক খুঁটিনাটি তথ্য তাই আৰ জানা যায়নি। যেমন তেওঁ বিয়ে কৰেআছিল কিনা, তেখেতৰ কোন সন্তান ছিল কিনা এসমূহৰ এখনো অজানা। যৌবনে আৰ্কিমিডিছ সম্ভবত মিসৰেৰ আলেকজান্দ্ৰিয়ায় পড়াশুনা কৰেআছিল, য’ত কোনোন অভ সামোস আৰু এৰাতোস্থেনেস অফ সিৰেন তেখেতৰ সহপাঠী আছিল। তেওঁ কোনোন অভ সামোসকে তেখেতৰ বন্ধু হিচাপে উল্লেখ কৰেআছিল; অপৰদিকে তেখেতৰ দুটি কাজেৰ ( দ্য মেথোড অভ মেকানিক্যাল থিওৰেমস আৰু দ্য ক্যাটল প্ৰবলেম) আৰম্ভতে এৰাতোস্থেনেসেৰ উদ্দেশ্যে কিছু নিৰ্দেশনা ছিল।সাঁচ:Ref label

২১২ খৃষ্টপূৰ্বাব্দে দ্বিতীয় পিউনিক যুদ্ধেৰ সময় আৰ্কিমিডিছ নিহত হন, যখন ৰোমান সেনাপতি জেনাৰেল মাৰ্কাস ক্লডিয়াস মাৰ্সেলাস দুই বছৰ ধৰে অবৰোধেৰ পৰ সিৰাকিউজ শহৰ দখল কৰে। প্লুটাৰ্খেৰ বিবৰণ অনুযায়ী, সিৰাকিউজেৰ পতনেৰ সময় আৰ্কিমিডিছ এটা গাণিতিক চিত্ৰ নিয়ে ব্যস্ত আছিল। এক ৰোমান সৈন্য তেঁওক কাজ বন্ধ কৰে জেনাৰেল মাৰ্সেলাসেৰ সৈতে দেখা কৰতে যাওয়াৰ নিৰ্দেশ দেয়। আৰ্কিমিডিছ তেখেতৰ কাজ শেষ না কৰে যেতে অস্বীকৃতি জানালে ক্ষিপ্ত সৈনিক তাৰ তলোয়াৰ দিয়ে তেঁওক তাৎক্ষণিকভাবে হত্যা কৰে। অন্য এটা স্বল্প প্ৰচলিত ধাৰণা হৈছে, আৰ্কিমিডিছ এক ৰোমান সৈন্যেৰ কাষত আত্মসমৰ্পণেৰ সময় নিহত হন। এই মতবাদ অনুসাৰে, তেওঁ কিছু গাণিতিক সৰঞ্জাম বহন কৰআছিল যেসমূহৰকে সৈন্যটি মূল্যবান সম্পদ ভেবে বিভ্ৰান্ত হয় আৰু লোভে পড়ে তেঁওক হত্যা কৰে। বলা হয়ে থাকে যে, জেনাৰেল মাৰ্সেলাস আৰ্কিমিডিছৰ বৈজ্ঞানিক প্ৰতিভা সম্পৰ্কে অবগত আছিল আৰু তেওঁ তেখেতৰ কোন ক্ষতি না কৰাৰ বাবে নিৰ্দেশ দিয়েআছিল। আৰ্কিমিডিছৰ মৃত্যুসংবাদ তাই তেঁওক ক্ষুব্ধ কৰে।

কোন গোলকেৰ আয়তন আৰু পৃষ্ঠতলেৰ ক্ষেত্ৰফল তাৰ অন্তঃস্থ সিলিণ্ডাৰেৰ আয়তন ও পৃষ্ঠতলেৰ ২/৩ অংশেৰ সমান। আৰ্কিমিডিছৰ সমাধিতে তেখেতৰ নিজেৰ অনুৰোধে এটা গোলক ও এটা সিলিণ্ডাৰ বসানো হয়।

আৰ্কিমিডিছৰ সমাধিফলকে এটা ভাস্কৰ্য ৰৈছে যা সমান উচ্চতা ও ব্যাসেৰ এটা গোলক ও এটা সিলিণ্ডাৰ নিয়ে গঠিত, যা তেখেতৰ সবাতোকৈ বিখ্যাত আবিষ্কাৰসমূহৰৰ এটাকে নিৰ্দেশ কৰে। তেওঁ প্ৰমাণ কৰেআছিল যে সমান উচ্চতা ও ব্যাসবিশিষ্ট এটা গোলক ও এটা সিলিণ্ডাৰেৰ ক্ষেত্ৰে গোলকটিৰ আয়তন ও পৃষ্ঠতলেৰ ক্ষেত্ৰফল সিলিণ্ডাৰেৰ আয়তন ও পৃষ্ঠতলেৰ ক্ষেত্ৰফলেৰ দুই তৃতীয়াংশ। আৰ্কিমিডিছৰ মৃত্যুৰ ১৩৭ বছৰ পৰ ৭৫ খৃষ্টাব্দে ৰোমান বক্তা সিসেৰো সিৰাকিউজেৰ এগ্ৰিজেনটিন গেইটেৰ কাষত ঝোপঝাড় পৰিবেষ্টিত অবস্থায় আৰ্কিমিডিছৰ কবৰ আবিষ্কাৰ কৰে।

আবিষ্কাৰ ও উদ্ভাবনসমূহ

সোনাৰ মুকুট

আৰ্কিমিডিছ তাৰ অনিয়মিত আকাৰেৰ বস্তুৰ আয়তন পৰিমাপেৰ পদ্ধতিৰ মাধ্যমে প্ৰমাণ কৰে যে মুকুটেৰ সোনাৰ ঘনত্ব খাটি সোনাৰ ঘনত্বেৰ চেয়ে কম।

আৰ্কিমিডিছৰ সবাতোকৈ জনপ্ৰিয় আবিষ্কাৰসমূহৰৰ মাজত এটা ছিল অনিয়মিত আকাৰেৰ বস্তুৰ আয়তন পৰিমাপেৰ পদ্ধতি। ভিট্ৰুভিয়াসেৰ বিবৰণ অনুযায়ী, ৰাজা দ্বিতীয় হিয়েৰোৰ বাবে লৰেল পাতাৰ মুকুটেৰ মত দেখতে এটা সোনাৰ মুকুট প্ৰস্তুত কৰা হয়েছিল। আৰ্কিমিডিছকে দায়িত্ব দেয়া হয়েছিল মুকুটটি খাঁটি সোনাৰ কিনা সেটা নিশ্চিত কৰাৰ। সহজ পদ্ধতি ছিল মুকুটটি গলিয়ে তাৰ ঘনত্ব নিৰ্ণয় কৰা, কিন্তু ৰাজা মুকুটটি নষ্ট কৰতে ৰাজি আছিল না। আৰ্কিমিডিছ যখন এ সমস্যা নিয়ে ভাবআছিল, তখন হঠাৎ গোসল কৰতে গিয়ে তেওঁ লক্ষ্য কৰে যে তেওঁ পানিতে নামা মাত্ৰে বাথটাবেৰ পানিৰ উচ্চতা বৃদ্ধি পাচ্ছে। তেওঁ বুঝতে পাৰেন যে পানিৰ এই ধৰ্মকে ঘনত্ব পৰিমাপে ব্যবহাৰ কৰা সম্ভব। যেহেতু ব্যবহাৰিক কাজেৰ বাবে পানি অসংকোচনশীল, তাই পানিতে নিমজ্জিত মুকুট তাৰ আয়তনেৰ সমান পৰিমাণ পানি স্থানচ্যুত কৰবে। এই অপসাৰিত পানিৰ আয়তন দ্বাৰা মুকুটেৰ ভৰকে ভাগ কৰে মুকুটেৰ ঘনত্ব পৰিমাপ কৰা সম্ভব। যদি মুকুটেৰ উপাদানে সোনাৰ সৈতে অন্য কোন কম ঘনত্বেৰ সস্তা ধাতু যোগ কৰা হয় তাহলে তাৰ ঘনত্ব খাঁটি সোনাৰ ঘনত্বেৰ চেয়ে কম হবে। বলা হয়ে থাকে যে এই আবিষ্কাৰ আৰ্কিমিডিছকে এতই উত্তেজিত কৰেছিল যে তেওঁ নগ্ন অবস্থায় শহৰেৰ ৰাস্তায় "ইউৰেকা" (গ্ৰিক: "εὕρηκα!" ; অৰ্থ "আমি পেয়েছি!") বলে চিৎকাৰ কৰতে কৰতে দৌড়াতে আৰম্ভ কৰেআছিল।

বাস্তবে আৰ্কিমিডিছৰ আবিষ্কৃত এই পদ্ধতিটি প্ৰশ্নেৰ সম্মুখীন হয়েছিল, কাৰণ ঘনত্বেৰ পাৰ্থক্যেৰ কাৰণে যে পৰিমাণ পানি অপসাৰিত হবে সেটি সঠিকভাবে নিৰ্নয় কৰা এটা কষ্টসাধ্য কাজ।এই সমস্যাৰ সমাধান কৰা হয় হয় fluid statics এৰ মাধ্যমে যেটি আৰ্কিমিডিছ তত্ত্ব নামে পৰিচিত। তত্ত্বটি তাৰ On Floating Bodies প্ৰবন্ধে বৰ্ণনা কৰা হৈছে। তত্ত্বে বলা হৈছে যে , কোন বস্তুৰ ওজন এটি দ্বাৰা অপসাৰিত পানিৰ ওজনেৰ সমান।

আৰ্কিমিডিছৰ স্ক্ৰু

আৰ্কিমিডিছৰ স্ক্ৰু পানি উত্তলনেৰ কাজ ব্যবহৃত একট কাৰ্যকৰ যন্ত্ৰ।

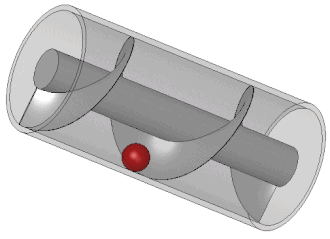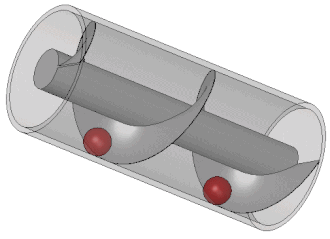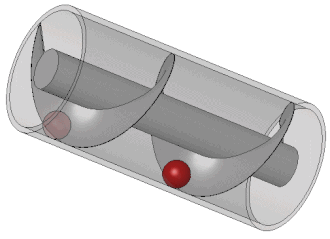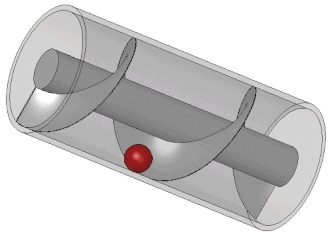
আৰ্কিমিডিছৰ প্ৰকৌশল কাজেৰ অধিকাংশই ছিল তেখেতৰ নিজ শহৰ সিৰাকিউজেৰ প্ৰয়োজন মেটানোৰ বাবে। গ্ৰিক লেখক অথেনিয়াস অভ নক্ৰেটিসেৰ বৰ্ণনা অনুযায়ী, ৰাজা দ্বিতীয় হিয়েৰো আৰ্কিমিডিছকে এটা বিশাল জাহাজ তৈৰি কৰাৰ দায়িত্ব দিয়েআছিল। সিৰাকিউসা নামেৰ এই জাহাজটিকে প্ৰয়োজনানুযায়ী প্ৰমোদতৰী, ৰসদ-সৰবৰাহকাৰী আৰু ৰণতৰী হিচাপে ব্যবহাৰ কৰে যেত। বলা হয়ে থাকে যে ক্লাসিকাল যুগে নিৰ্মাণ কৰা সকল জাহাজেৰ মাজত সিৰাকিউসা ই ছিল সৰ্ববৃহৎ। অথেনিয়াসেৰ ধাৰণামতে, এই জাহাজে একসৈতে ছয়শো যাত্ৰী বহন কৰা যেত আৰু জাহাজটিতে সাজানো বাগান, এটা ব্যায়ামাগাৰ আৰু দেৱী আফ্ৰোদিতিৰ মন্দিৰ ছিল। স্বাভাবিকভাবেই এত বৃহদাকৃতিৰ এটা জাহাজে প্ৰচুৰ পানি চুঁইয়ে ঢুকতো। সেই পানি নিৰ্গমণেৰ বাবে আৰ্কিমিডিছ তেখেতৰ বিখ্যাত আৰ্কিমিডিছৰ স্ক্ৰু তৈৰি কৰে। এটি ছিল প্ৰকৃতপক্ষে এটা সিলিণ্ডাৰেৰ ভেতৰে আবদ্ধ এটা স্ক্ৰু আকৃতিৰ ঘূৰ্ণায়মান ধাতব ব্লেড যাকে হাত দিয়ে ঘুৰানো হত। এই যন্ত্ৰটি খাল পৰা উঁচু জমিতে সেচেৰ বাবেও ব্যবহাৰ কৰা হত। বৰ্তমানকালেও পানি আৰু কয়লা, শস্যদানা জাতীয় ক্ষুদ্ৰাকৃতিৰ পদাৰ্থ উত্তোলনেৰ বাবে আৰ্কিমিডিছৰ স্ক্ৰু ব্যবহাৰ কৰা হয়। ভিট্ৰুভিয়াসেৰ বিবৰণ অনুযায়ী, আৰ্কিমিডিছৰ স্ক্ৰু সম্ভবত প্ৰাচীন ব্যবিলনেৰ শূণ্যোদ্যানে জলসেচনেৰ বাবে ব্যবহৃত স্ক্ৰু পাম্পেৰ এটা উন্নততৰ ৰূপ ছিল।

আৰ্কিমিডিছৰ থাবা

"দ্য ক্ল অভ আৰ্কিমিডিছ" বা "আৰ্কিমিডিছৰ থাবা" এটা অস্ত্ৰ যা আৰ্কিমিডিছ তেখেতৰ শহৰ সিৰাকিউজকে বহিঃস্থ আক্ৰমণ পৰা ৰক্ষাৰ বাবে উদ্ভাবন কৰেআছিল বলে বলা হয়ে থাকে। এ যন্ত্ৰটিতে এটা ক্ৰেনেৰ ন্যায় বাহু আৰু তাতে ঝুলানো এটা বিশাল ধাতব আংটা ছিল। এই আংটাৰ সহায়ে আক্ৰমণকাৰী জাহাজকে উল্টে ফেলা হত। আধুনিককালে এই যন্ত্ৰেৰ কাৰ্যকাৰিতা নিয়ে বেশ কিছু পৰীক্ষা কৰা হৈছে। ২০০৫ চনত "সুপাৰউইপনস অভ দ্য এনসিয়েন্ট ওয়াৰ্ল্ড" নামেৰ এটা টেলিভিশন ডকুমেণ্টাৰীতে এমন এটা যন্ত্ৰ প্ৰস্তুত কৰা হয় আৰু সিদ্ধান্ত দেয়া হয় যে এটি প্ৰস্তুত আৰু সাৰ্থকভাবে ব্যবহাৰ কৰা সম্ভব।

আৰ্কিমিডিছৰ উত্তপ্ত ৰশ্মিঃ সত্য নাকি জনশ্ৰুতি?

আৰ্কিমিডিছ হয়তো অনেকসমূহৰ আয়না একত্ৰ কৰে আবতল প্ৰতিফলক হিচাপে কাজ কৰিয়ে সিৰাকিউজ আক্ৰমণকাৰী জাহাজ ভস্মীভূত কৰেআছিল।

দ্বিতীয় শতকেৰ লেখক লুসিয়ানেৰ বৰ্ণনা অনুযায়ী, সিৰাকিউজ যখন আক্ৰান্ত হয়, আৰ্কিমিডিছ শত্ৰুপক্ষেৰ জাহাজ আগুনে ভস্মীভূত কৰে। ট্ৰেলসেৰ এনথেমিয়াসেৰ বিবৰণ অনুযায়ী, আৰ্কিমিডিছ অনেকগুলি আয়নাৰ সহায়ে আক্ৰমণকাৰী জাহাজেৰ উপৰ সূৰ্যৰশ্মি কেন্দ্ৰীভূত কৰে সেসমূহৰতে অগ্নিসংযোগ কৰে।

ৰেনেসাঁ যুগ পৰাই অবশ্য এই জনশ্ৰুতিৰ সত্যতা নিয়ে বিতৰ্ক চলে আসছে। ৰেনে দেকাৰ্ত একে অসত্য বলে প্ৰত্যাখ্যান কৰিছে, যদিও বৰ্তমানকালেৰ বিজ্ঞানীৰা শুধুমাত্ৰ আৰ্কিমিডিছৰ যুগে সহজলভ্য যন্ত্ৰপাতিৰ সহায়ে এই প্ৰক্ৰিয়াৰ সম্ভাব্যতা যাচাই কৰাৰ চেষ্টা কৰে যাচ্ছেন। অনেকেৰ ধাৰণা, সাৰিবদ্ধভাবে সাজানো অনেকসমূহৰ চকচকে পলিশ কৰা ব্ৰোঞ্জ বা তামাৰ পাতেৰ সহায়ে জাহাজেৰ উপৰ সূৰ্যৰশ্মি কেন্দ্ৰীভূত কৰা সম্ভব। এতে প্ৰকৃতপক্ষে সৌৰচুল্লীতে ব্যবহৃত পৰাবৃত্তিক প্ৰতিফলনেৰ নীতি ব্যবহাৰ কৰা হবে।

১৯৭৩ চনত গ্ৰিক বিজ্ঞানী ইওয়ান্নিস সাক্কাস আৰ্কিমিডিছৰ সূৰ্যৰশ্মি নিয়ে এটা পৰীক্ষা চালান। এ পৰীক্ষায় তেওঁ সত্তুৰটি আয়না ব্যবহাৰ কৰে। প্ৰতিটি আয়নাৰ আকাৰ ছিল পাঁচ ফুট বনাম তিন ফুট আৰু এসমূহৰ তামা দ্বাৰা পালিশ কৰা ছিল। আয়নাসমূহৰ একশো ষাট ফুট দূৰবৰ্তী এটা প্লাইউড নিৰ্মিত জাহাজেৰ দিকে তাক কৰা ছিল। আয়নাসমূহৰ ঠিকমত ফোকাস কৰাৰ মাত্ৰ কয়েক সেকেণ্ডেৰ মাজত জাহাজটিতে আগুন ধৰে যায়। অবশ্য জাহাজটিতে আলকাতৰাৰ প্ৰলেপ ছিল, যা সম্ভবত অগ্নিসংযোগেৰ সহায়ক হিচাপে কাজ কৰেছে।

২০০৫ এৰ অক্টোবৰে ম্যাসাচুসেটস ইন্সটিটিউট অভ টেকনোলজিৰ একদল ছাত্ৰ ১২৭টি এক ফুট দৈৰ্ঘ্য-প্ৰস্থ বিশিষ্ট আয়না প্ৰায় ১০০ ফুট দূৰবৰ্তী এটা কাঠেৰ ডামি জাহাজেৰ উপৰ ফোকাস কৰে এটা পৰীক্ষা চালায়। প্ৰায় দশ মিনিট ঊজ্জ্বল সূৰ্যালোকে এক জায়গায় থাকাৰ পৰ জাহাজটিতে আগুন জ্বলে ওঠে। এ পৰীক্ষা পৰা সিদ্ধান্তে আসা হয় যে এ প্ৰক্ৰিয়ায় অগ্নিসংযোগ সম্ভব তবে তা শুধুমাত্ৰ কিছু নিৰ্দিষ্ট পৰিস্থিতিতে। মিথবাষ্টাৰ্স টেলিভিশন শোতে এমআইটিৰ এই শিক্ষাৰ্থীৰা পুনৰায় একই পৰীক্ষা চালায়, এবাৰ সানফ্ৰান্সিসকো ঊপকূলে এটা কাঠেৰ মাছধৰা নৌকাৰ উপৰ। এবাৰও বেশ কিছু সময় পৰ ছোট আকাৰে নৌকাটিতে আগুন জ্বলে ওঠে। প্ৰকৃতপক্ষে আগুন জ্বলে ওঠাৰ বাবে কাঠকে তাৰ দহন তাপমাত্ৰায় পৌছতে হয় যা প্ৰায় তিনশো ডিগ্ৰি সেলসিয়াসেৰ সমান।

২০০৬ এৰ জানুৱাৰীতে অনুষ্ঠানটি সম্প্ৰচাৰেৰ সময় মীথবাষ্টাৰ্স সিদ্ধান্ত দেয় যে এটি প্ৰকৃতপক্ষে জনশ্ৰুতি, সত্য নয়। এৰ স্বপক্ষে যুক্তি হিচাপে অগ্নিসংযোগেৰ বাবে দীৰ্ঘ সময় আৰু ঊজ্জ্বল সূৰ্যালোকেৰ প্ৰয়োজনীয়তাৰ দিকে নিৰ্দেশ কৰা হয়। ইয়াৰ বাদেওও বলা হয় যে সিৰাকিউজ পূৰ্বদিক পৰা আক্ৰান্ত হয়েছিল, সেক্ষেত্ৰে শুধুমাত্ৰ সকাল বেলাৰ আক্ৰমণই এ পদ্ধতিতে মোকাবেলা কৰা সম্ভব। মীথবাষ্টাৰ্সে এ কথাও মনে কৰিয়ে দেয়া হয় যে সেসময় প্ৰচলিত অন্যান্য অস্ত্ৰ, যেমন অগ্নিসংযোগ কৰা তীৰ অথবা ক্যাটাপোল্টেৰ বোল্ট ব্যবহাৰ কৰে আৰো সহজে কোন জাহাজে দূৰ পৰা অগ্নিসংযোগ কৰা সম্ভব ছিল।

অন্যান্য আবিষ্কাৰ ও উদ্ভাবন

যদিও আৰ্কিমিডিছ নিজে লিভাৰ উদ্ভাবন কৰেি, তেওঁই প্ৰথম লিভাৰেৰ কাৰ্যনীতি নিয়ে বিস্তাৰিত আলোচনা কৰে। পাপ্পাস অভ আলেকজান্দ্ৰিয়াৰ কথা অনুযায়ী, লিভাৰেৰ মূলনীতি বোঝাতে গিয়ে আৰ্কিমিডিছ বলেআছিল, "আমাকে একটা দাঁড়ানোৰ জায়গা দাও, আমি পৃথিৱীকে তুলে সৰিয়ে দেব"। প্লুটাৰ্খ ব্যাখ্যা কৰিছে আৰ্কিমিডিছ কিভাবে ব্লক-এণ্ড-ট্যাকল পুলি ডিজাইন কৰে, যা নাবিকদেৰ লিভাৰেৰ মুলনীতি ব্যবহাৰ কৰে অনেক ভাৰী বস্তু সৰাতে সহায় কৰে। ইয়াৰ বাদেওও আৰ্কিমিডিছ ক্যাটাপোল্টেৰ ক্ষমতা আৰু দক্ষতা বৃদ্ধি কৰে আৰু প্ৰথম পিউনিক যুদ্ধেৰ সময় ওডোমিটাৰ আবিষ্কাৰ কৰে। প্ৰচলিত বিবৰণ অনুযায়ী, ওডোমিটাৰ ছিল এটা গীয়াৰযুক্ত ঠেলাগাড়ি যা প্ৰতি মাইল চলাৰ পৰ এটা পাত্ৰে ছোট এটা গোলক ফেলে দিত।

সিসেৰো (খৃষ্টপূৰ্ব ১০৬ - ৪৩) তেখেতৰ De re publica নামক কাল্পনিক কথোপকথনে আৰ্কিমিডিছৰ উল্লেখ কৰে। সিৰাকিউজ দখলেৰ পৰ ৰোমান সেনাপতি মাৰ্কাস ক্লদিয়াস মাৰ্সেলাস ৰোমে দুটি যন্ত্ৰ নিয়ে যান। এই যন্ত্ৰগুলিৰ সহায়ে সূৰ্য, চাঁদ আৰু পাঁচটি গ্ৰহেৰ স্থান পৰিবৰ্তন দেখানো যেত, যা জ্যোতিৰ্বিদ্যায় ব্যবহৃত হত।}} একসময় ধাৰণা কৰা হত যে এমন যন্ত্ৰ তৈৰি কৰাৰ বাবে যে পৰিমাণ যন্ত্ৰকৌশলগত জ্ঞান থাকা লাগে তা এত প্ৰাচীনকালে ছিল না, কিন্তু ১৯০২ চনত এন্টিকাইথেৰা মেকানিজমেৰ খোঁজ পোৱাৰ পৰ বোঝা যায় যে প্ৰাচীন গ্ৰিকদেৰ এসব বিষয়ে যথেষ্ট জ্ঞান ছিল।

গণিত

যদিও আৰ্কিমিডিছকে বিভিন্ন যন্ত্ৰ আবিষ্কাৰেৰ বাবে সবাতোকৈ বেছি মনে ৰাখা হয়, কিন্তু তেওঁ গণিতেও অনেক অবদান ৰাখেন। প্লুটাৰ্খ লিখেছেন, "তেখেতৰ সমুদয় ভালোবাসা আৰু উচ্চাকাঙ্খা ছিল সেসব তাত্ত্বিক বিষয়েৰ প্ৰতি য’ত তেঁওক বাস্তব জীৱনেৰ প্ৰয়োজন নিয়ে মাথা ঘামাতে হতো না।"

আৰ্কিমিডিছ মেথড অভ এক্সহশন ব্যবহাৰ কৰে পাইয়েৰ আসন্ন মান নিৰ্ণয় কৰে

আৰ্কিমিডিছ বৰ্তমানে ইন্টিগ্ৰ্যাল ক্যালকুলাসে ব্যবহৃত অতিক্ষুদ্ৰ সংখ্যাৰ ধাৰণা ব্যবহাৰ কৰতে সক্ষম আছিল। প্ৰুফ অভ কন্ট্ৰাডিকশন ব্যবহাৰ কৰে তেওঁ নিখুঁতভাবে বিভিন্ন গাণিতিক সমস্যাৰ সমাধান কৰতে পাৰতেন, সেই সৈতে সেসব সমাধানেৰ লিমিটও উল্লেখ কৰিছিল। এই পদ্ধতিকে বলা হয় মেথড অভ এক্সহশন, যাৰ সহায়ে তেওঁ পাইয়েৰ মান যথেষ্ট নিখুঁতভাবে নিৰ্ণয় কৰে। তেওঁ এই কাজেৰ বাবে বৃত্তেৰ বাইৰে এটা বড় বহুভুজ আৰু ভেতৰে এটা ছোট বহুভুজ আঁকেন। বহভুজেৰ বাহুৰ সংখ্যা যত বৃদ্ধি পায়, তা আকৃতিতে বৃত্তেৰ তত কাছাকাছি আসতে থাকে। যখন প্ৰতিটি বহুভুজেৰ ৯৬টি কৰে বাহু, তেওঁ বহুগুলিৰ দৈৰ্ঘ্য নিৰ্ণয় কৰে আৰু দেখান যে পাইয়েৰ মান ৩১/৭ (প্ৰায় ৩.১৪২৯) আৰু ৩১০/৭১ (প্ৰায় ৩.১৪০৮) এৰ মাঝে, যা প্ৰকৃত মান ৩.১৪১৬ এৰ খুগ্ৰন্থ কাছাকাছি। তেওঁ আৰও প্ৰমাণ কৰে যে বৃত্তেৰ ক্ষেত্ৰফল তাৰ ব্যাসাৰ্ধেৰ বৰ্গেৰ পাই গুণিতকেৰ সমান। অন দ্য স্ফীয়াৰ এণ্ড সিলিণ্ডাৰ গ্ৰন্থতে তেওঁ মতবাদ প্ৰদান কৰে যে, যে কোন মানকে তাৰ নিজেৰ সৈতে যথেষ্ট সংখ্যক বাৰ যোগ কৰলে তা যে কোন নিৰ্দিষ্ট মানকে অতিক্ৰম কৰবে। এই মতবাদ বাস্তব সংখ্যাৰ আৰ্কিমিডিয়ান বৈশিষ্ট্য নামে পৰিচিত।

মেজাৰমেন্ট অভ সাৰ্কেল গ্ৰন্থতে আৰ্কিমিডিছ ৩ এৰ বৰ্গমূল ২৬৫/১৫৩ (প্ৰায় ১.৭৩২০২৬১) আৰু ১৩৫১/৭৮০ (প্ৰায় ১.৭৩২০৫১২) এৰ মাঝে বলে উল্লেখ কৰে, যা প্ৰকৃত মান ১.৭৩২০৫৮ এৰ খুগ্ৰন্থ কাছাকাছি। তেওঁ অবশ্য কোন পদ্ধতিতে এই মান নিৰ্ণয় কৰেআছিল সে প্ৰসঙ্গে কোন কিছুই উল্লেখ কৰেি।

আৰ্কিমিডিছ প্ৰমাণ কৰিছে যে উপৰেৰ চিত্ৰেৰ পৰাবৃত্তিক ক্ষেত্ৰটিৰ ক্ষেত্ৰফল নিচেৰ চিত্ৰেৰ অন্তঃস্থ ত্ৰিভুজটিৰ ক্ষেত্ৰফলেৰ ৪/৩ গুণিতকেৰ সমান।

কোয়াড্ৰেচাৰ অভ প্যাৰাবোলা গ্ৰন্থতে আৰ্কিমিডিছ প্ৰমাণ কৰে যে এটা পৰাবৃত্ত আৰু এটা সৰলৰেখা দ্বাৰা আবদ্ধ ক্ষেত্ৰে ক্ষেত্ৰফল একই ক্ষেত্ৰেৰ অন্তঃস্থ ত্ৰিভুজেৰ ক্ষেত্ৰফলেৰ ৪/৩ গুণিতকেৰ সমান, যা পাশেৰ চিত্ৰে দেখানো হৈছে। তেওঁ এ সমস্যাৰ সমাধানটিকে এটা অসীম ধাৰা হিচাপে প্ৰকাশ কৰে যাৰ সাধাৰণ অনুপাত ১/৪।

$\sum _{n=0}^{\mathrm{\infty }}{4}^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots =\frac{4}{3}.$

দ্য স্যাণ্ড ৰেকোনাৰ গ্ৰন্থতে আৰ্কিমিডিছ এই মহাবিশ্ব মোটা কতসমূহৰ ধূলিকণা ধাৰণ কৰতে সক্ষম তা গণনা কৰাৰ চেষ্টা কৰে। এৰ মাধ্যমে তেওঁ ধূলিকণাৰ সংখ্যা গণনা কৰাৰ বাবে অনেক বেছি বড় এই ধাৰণাকে চ্যালেঞ্জ কৰে। এ সমস্যা সমাধানেৰ উদ্দেশ্যে তেওঁ মিৰিয়াডেৰ ভিত্তিতে গণনা কৰাৰ এটা পদ্ধতি বেৰ কৰে। মিৰিয়াড শব্দটি গ্ৰিক μυριάς murias পৰা উদ্ভূত, যাৰ অৰ্থ ১০,০০০। তেওঁ ১০০ মিলিয়নকে (মিৰিয়াডেৰ মিৰিয়াড) ভিত্তি কৰে এটা নাম্বাৰ সিষ্টেম প্ৰস্তাব কৰে আৰু সিদ্ধান্তে উপনীত হন যে মহাবিশ্বকে সম্পূৰ্ণভাবে পূৰ্ণ কৰতে ৮ ভিজিনটিলিয়ন ( ৮ x ১০^৬৩) ধূলিকণা প্ৰয়োজন।

লেখালেখি

আৰ্কিমিডিছ তাৰ কাজেৰ লিখিত ৰূপেৰ বাবে ডৰিক গ্ৰিক ভাষা ব্যবহাৰ কৰিছিল, যা প্ৰাচীন সিৰাকিউজেৰ আঞ্চলিক ভাষা হিচাপে প্ৰচলিত ছিল। . আৰ্কিমিডিছৰ অধিকাংশ কাজ ইউক্লিডেৰ কাজেৰ মত সংৰক্ষিত হয়নি; তেখেতৰ সাতটি থীসিসেৰ কথা জানা যায় কেবলমাত্ৰ অন্যদেৰ কাজেৰ ৰেফাৰেন্স পৰা। পাপ্পাস অভ আলেকজান্দ্ৰিয়া আৰ্কিমিডিছৰ "অন স্ফীয়াৰ মেকিং" আৰু বহুতল বিশিষ্ট বস্তুৰ উপৰ আৰএটা কাজেৰ কথা উল্লেখ কৰিছে। অপৰদিকে থেৰন অভ আলেকজান্দ্ৰিয়া প্ৰতিসৰণ সম্পৰ্কে আৰ্কিমিডিছৰ হাৰিয়ে যাওয়া এটা লেখনী "Catoptrica" এৰ উল্লেখ কৰে। জীবদ্দশায় আৰ্কিমিডিছ তেখেতৰ কাজেৰ প্ৰচাৰেৰ বাবে আলেকজান্দ্ৰিয়াৰ গণিতবিদদেৰ উপৰ নিৰ্ভৰ কৰিছিল। বাইজান্টাইন স্থপতি ইসিডোৰ অভ মিলেতাস আৰ্কিমিডিছৰ লেখনীসমূহৰকে একত্ৰিত কৰে; পৰৱৰ্তীতে ষষ্ঠ শতকে ইউতোশিয়াস অভ আসকালোন তেখেতৰ কাজেৰ উপৰ লিখিত বিবৰণ প্ৰকাশ কৰাৰ পৰ আৰ্কিমিডিছৰ কাজ বৃহত্তৰ জনগোষ্ঠীৰ কাষত পৰিচিত হয়ে ওঠে। আৰ্কিমিডিছৰ কাজ থাবিত ইবনে কুৰৰা (৮৩৬-৯০১ খৃষ্টাব্দ) আৰবিতে আৰু জেৰাৰ্ড অভ ক্ৰেমোনা (১১৪৭-১১৮৭ খৃষ্টাব্দ) ল্যাটিনে অনুবাদ কৰে। ৰেনেসাঁৰ সময় ১৫৪৪ চনত জোহান হেৰওয়াগেন সুইজাৰল্যাণ্ডেৰ বাজল শহৰ পৰা গ্ৰিক ও ল্যাটিন ভাষায় আৰ্কিমিডিছৰ কাজ সহ এডিটিও প্ৰিন্সেপস (Editio Princeps) গ্ৰন্থয়েৰ প্ৰথম সংস্কৰণ প্ৰকাশ কৰে। ১৫৮৬ চনত গ্যালিলিও গ্যালিলি বাতাস ও পানিতে ধাতব বস্তুৰ ওজন নিৰ্ণয়েৰ বাবে এটা হাইড্ৰোষ্ট্যাটিক নিক্তি উদ্ভাবন কৰে, যা আৰ্কিমিডিছৰ কাজ দ্বাৰা অনুপ্ৰাণিত বলে বলা হয়ে থাকে।

অক্ষত কাজসমূহ

লিভাৰ সম্পৰ্কে আৰ্কিমিডিছৰ কথিত উক্তি, "আমাকে একটা দাঁড়ানোৰ জায়গা দাও, আমি পৃথিৱীকে তুলে সৰিয়ে দেব"

• অন দ্য ইকুইলিব্ৰিয়াম অভ প্লেইনস (On the Equilibrium of Planes) (দুই খণ্ড)

প্ৰথম খণ্ডে পনেৰটি উপপাদ্য আৰ সাতটি অনুসিদ্ধান্ত ৰৈছে, অপৰদিকে দ্বিতীয় খণ্ডে দশটি উপপাদ্য পোৱা যায়। এই গ্ৰন্থতে আৰ্কিমিডিছ লিভাৰেৰ মূলনীতি ব্যাখ্যা কৰে। তেওঁ বলেন, "লিভাৰেৰ দুই বাহুতে প্ৰযুক্ত ওজন বাহু দুইটিৰ দৈৰ্ঘ্যেৰ ব্যস্তানুপাতিক।"

এই গ্ৰন্থয়ে উল্লিখিত মূলনীতিৰ সহায়ে আৰ্কিমিডিছ বিভিন্ন জ্যামিতিক আকাৰেৰ বস্তু, যেমন ত্ৰিভুজ, সামান্তৰিক, পৰাবৃত্তেৰ ক্ষেত্ৰফল আৰু ভৰকেন্দ্ৰ নিৰ্ণয় কৰে।

• অন দ্য মেজাৰমেন্ট অভ আ সাৰ্কেল (On the Measurement of a Circle)

কোনন অভ সামোস (Conon of Samos) এৰ ছাত্ৰ ডোসিথিস অভ পেলুসিয়ামেৰ (Dositheus of Pelusium) সৈতে যৌথভাবে লিখিত এই প্ৰবন্ধে তিনটি উপপাদ্য ৰৈছে। দ্বিতীয় উপপাদ্যে আৰ্কিমিডিছ দেখান যে পাইয়েৰ মান ২২৩/৭১ এৰ চেয়ে বড় আৰু ২২/৭ এৰ চেয়ে ছোট। ২২/৭ কে পাইয়েৰ আসন্ন মান হিচাপে মধ্যযুগে গ্ৰহণ কৰা হয় আৰু বৰ্তমানেও অত্যন্ত নিখুঁত হিসাবেৰ প্ৰয়োজন না থাকলে ২২/৭ কেই পাইয়েৰ মান হিচাপে ব্যবহাৰ কৰা হয়ে থাকে।

• "অন স্পাইৰালস (On Spirals)"

আঠাশটি উপপাদ্য নিয়ে গঠিত এই কাজটিও ডোসিথিসকে উদ্দেশ্য কৰে লেখা। এখানে আনুষ্ঠানিকভাবে আৰ্কিমিডিয়ান স্পাইৰালকে সংজ্ঞায়িত কৰা হৈছে। এই সংজ্ঞা অনুযায়ী, পোলাৰ স্থানাঙ্ক ব্যবস্থায় ("r",θ) স্পাইৰালকে নিচেৰ সমীকৰণেৰ মাধ্যমে প্ৰকাশ কৰা যায়ঃ

$r=a+b\theta$

য’ত "a" আৰু "b" দুটি বাস্তব সংখ্যা।

• "অন দ্য স্ফীয়াৰ এ্যাণ্ড দ্য সিলিণ্ডাৰ (On the Sphere and the Cylinder)" (দুই খণ্ড)

ডোসিথিসকে উদ্দেশ্য কৰে লেখা এই উপপাদ্যে আৰ্কিমিডিছ সমান উচ্চতা আৰু ব্যাস বিসিষ্ট গোলক আৰু সিলিণ্ডাৰেৰ মধ্যবৰ্তী সম্পৰ্ক প্ৰকাশ কৰে। এই উপপাদ্য অনুযায়ী, "r" ব্যাসাৰ্ধবিশিষ্ট গোলক আৰু সিলিণ্ডাৰেৰ ক্ষেত্ৰে, গোলকেৰ আয়তন সাঁচ:Fracπr³ আৰু সিলিণ্ডাৰেৰ আয়তন 2πr³। অপৰদিকে, গোলকেৰ পৃষ্ঠতলেৰ ক্ষেত্ৰফল 4πr² আৰু সিলিণ্ডাৰেৰ পৃষ্ঠতলেৰ ক্ষেত্ৰফল 6πr²। গোলকটিৰ আয়তন আৰু পৃষ্ঠতলেৰ ক্ষেত্ৰফল যথাক্ৰমে সিলিণ্ডাৰেৰ আয়তন আৰু পৃষ্ঠতলেৰ ক্ষেত্ৰফলেৰ সাঁচ:Nowrap অংশ। উল্লেখ্য, আৰ্কিমিডিছ নিজেৰ এই কাজটি নিয়ে সৰ্বাপেক্ষা বেছি গৰ্ববোধ কৰিছিল আৰু তেখেতৰ মৃত্যুৰ পৰ তেখেতৰ অনুৰোধে তেখেতৰ সমাধিফলকেৰ উপৰ এটা গোলক আৰু এটা সিলিণ্ডাৰ স্থাপন কৰা হয়।

• "অন কোনয়েডস এ্যাণ্ড স্পেৰোয়েডস (On Conoids and Spheroids)"

বত্ৰিশটি উপপাদ্য সম্বলিত এই কাজটিও ডোসিথিয়াসকে উদ্দ্যেশ্য কৰে লেখা। এতে আৰ্কিমিডিছ কোণক, গোলক আৰু পৰাবৃত্তিক গোলকেৰ পৃষ্ঠতলেৰ ক্ষেত্ৰফল আৰু আয়তন পৰিমাপ কৰে।

• "অন ফ্লোটিং বডিজ (On Floating Bodies)" (দুই খণ্ড)

প্ৰথম খণ্ডে আৰ্কিমিডিছ প্ৰবাহী পদাৰ্থেৰ সাম্যাবস্থাৰ সূত্ৰ বিবৃত কৰে আৰু প্ৰমাণ কৰে যে পানি এটা ভাৰকেন্দ্ৰেৰ চাৰপাশে গোলকীয় আকাৰ ধাৰণ কৰবে। তেখেতৰ এই কাজটি সমসাময়িক গ্ৰীক জ্যোতিৰ্বিদদেৰ (যেমন এৰাতোস্থেনিস) "পৃথিৱী গোল" মতবাদেৰ ব্যাখ্যা কৰাৰ চেষ্টা পৰা হয়ে থাকতে পাৰে। তেওঁ এমন এটা বিন্দু কল্পনা কৰেআছিল যাৰ দিকে সকল পদাৰ্থ পতিত হয় আৰু গোলকীয় আকাৰ লাভেৰ চেষ্টা কৰে।

দ্বিতীয় খণ্ডে তেওঁ পৰাবৃত্তিক গোলকেৰ বিভিন্ন অংশেৰ সাম্যাবস্থামূলক অবস্থান পৰিমাপ কৰে। সম্ভবত তেখেতৰ চেষ্টা ছিল জাহাজেৰ হালেৰ এটা আদৰ্শ আকৃতি নিৰ্ণয় কৰা। তেখেতৰ কাজ কৰা পৰাবৃত্তিক গোলকগুলিৰ মাজত কিছু তাদেৰ ভূমি পানিৰ নিচে এখন শীৰ্ষ পানিৰ উপৰে ৰেখে ভাসতে পাৰতো, যেভাবে হিমশৈল সাগৰে ভেসে বেড়ায়। আৰ্কিমিডিছ এই গ্ৰন্থয়ে তেখেতৰ প্লবতাৰ নীতি বিবৃত কৰে এভাবেঃসাঁচ:Quote

• "দ্য কোয়াড্ৰেচাৰ অভ প্যাৰাবোলা(The Quadrature of the Parabola)"

ডোসিথিয়াসকে উদ্দেশ্য কৰে লেখা চব্বিশটি উপপাদ্য সম্বলিত এই ৰচনায় আৰ্কিমিডিছ দুইটি ভিন্ন পদ্ধতিতে প্ৰমাণ কৰে যে এটা পৰাবৃত্ত আৰু এটা সৰলৰেখা দ্বাৰা আবদ্ধ ক্ষেত্ৰেৰ ক্ষেত্ৰফল সমান ভূমি ও উচ্চতাবিশিষ্ট ত্ৰিভুজেৰ ক্ষেত্ৰফলেৰ ৪/৩ গুণ। এই প্ৰমাণেৰ বাবে তেওঁ এটা জ্যামিতিক ধাৰাৰ অসীম পৰ্যন্ত যোগফল নিৰ্ণয় কৰে।