ত্বৰণ

সাঁচ:Sidebar with collapsible lists সময়ৰ লগত বেগৰ পৰিবৰ্তনৰ হাৰক পদাৰ্থ বিজ্ঞানত ত্বৰণ (ইংৰাজী: Acceleration) বুলি কোৱা হয়। একমাত্ৰিক স্থানত, ত্বৰণ হৈছে বস্তু এটাৰ দ্ৰুতিৰ বৃদ্ধিৰ নাইবা হ্ৰাসৰ হাৰ। যিহেতু বেগ হ’ল এবিধ ভেক্টৰ, গতিকে বেগৰ মান আৰু দিশ দুয়োটাৰে পৰিবৰ্তনৰ হাৰকে ত্বৰণে সূচায়। ত্বৰণৰ মাত্ৰা হৈছে L T ⁻²। SI একক পদ্ধতিত, মিটাৰ প্ৰতি বৰ্গছেকেণ্ডত(m/s²) ত্বৰণ জোখা হয়। (ঋণাত্মক ত্বৰণৰ অৰ্থাৎ মন্থৰণৰ মাত্ৰা/একক ত্বৰণৰ সৈতে একে। )

সাধাৰণ ভাষাত, দ্ৰুতিৰ বৃদ্ধিকেই ত্বৰণেৰে বুজোৱা হয় (বেগৰ মান); আনহাতে দ্ৰুতিৰ হ্ৰাসকেই মন্থৰণ বুলি কোৱা হয়। পদাৰ্থ বিজ্ঞানত বেগৰ দিশৰ পৰিবৰ্তনৰ হাৰকো ত্বৰণ বুলি কোৱা হয়: ঘূৰ্ণনশীল গতিৰ ক্ষেত্ৰত বেগৰ দিশৰ পৰিবৰ্তনে অভিকেন্দ্ৰিক(কেন্দ্ৰৰফালে) ত্বৰণৰ সূচনা কৰে; আনহাতে দ্ৰুতিৰ পৰিবৰ্তনৰ হাৰে স্পৰ্শকীয় ত্বৰণৰ সূচনা কৰে।

ধ্ৰুপদী বলবিজ্ঞানত,এটা ধ্ৰুৱক ভৰৰ বস্তুৰ ত্বৰণ বস্তুটোৰ ওপৰত ক্ৰিয়া কৰা মুঠ বলৰ সমানুপাতিক (নিউটনৰ দ্বিতীয় গতিসূত্ৰ):

$𝐅=m𝐚\to 𝐚=𝐅/m$

য’ত, F- হ’ল বস্তুটোৰ ওপৰত ক্ৰিয়া কৰা লব্ধবল, m- হৈছে বস্তুটোৰ ভৰ, আৰু a- হৈছে বস্তুটোৰ ত্বৰণ।

ত্বৰণ হৈছে বেগৰ পৰিৱৰ্তনৰ হাৰ, প্ৰক্ষেপণৰ যোকোনো বিন্দুত ত্বৰণৰ মান সেই বিন্দুত বেগৰ মান আৰু দিশৰ পৰিৱৰ্তনেৰে বুজোৱা হয়।

বক্ৰ সমতলীয় গতিৰ বাবে ত্বৰণৰ ঊপাংশ

গড় ত্বৰণ হ’ল বেগৰ পৰিবৰ্তন(Δv) হৰণ সময়ৰ পৰিবৰ্তন (Δt)।

তাৎক্ষণিক ত্বৰণ হৈছে এক বিশেষ মুহূৰ্তত (সময়ত) জোখা ত্বৰণ, যি মুহূৰ্তত ক্ষুদ্ৰ সময়ৰ অনুবন্ধ Δt শূন্যলৈ আগবাঢ়ে।

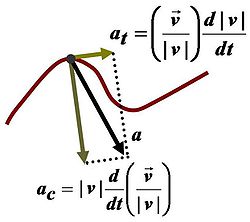
স্পৰ্শকীয় আৰু অভিকেন্দ্ৰিক ত্বৰণ

সাঁচ:See also বক্ৰপথত গতি কৰা যিকোনো পদাৰ্থ কণিকা এটাৰ বেগ সময়ৰ ফলন হিচাপে এনেদৰে লিখিব পাৰি:

$𝐯(t)=v(t)\frac{𝐯(t)}{v(t)}=v(t){𝐮}_{\mathrm{t}}(t),$

য’ত, v(t) য়ে বক্ৰপথত পদাৰ্থ কণিকাটোৰ বেগক সূচাইছে আৰু

${𝐮}_{\mathrm{t}}=\frac{𝐯(t)}{v(t)},$

এ সেইমুহূৰ্তত গতিপথৰ দিশত স্পৰ্শকীয় একক ভেক্টৰ সূচাইছে॥ সামতলিক ক্ষেত্ৰত বক্ৰপথত গতি কৰা পদাৰ্থ কণিকাৰ ত্বৰণ, দ্ৰুতিৰ পৰিবৰ্তন v(t) আৰু দিশৰ পৰিবৰ্তন u_t ক একেলগে লৈ, অৱকলনৰ শৃংখল নীতি আৰু সময়ৰ ফলন দুটাৰ পুৰণৰ অৱকলন হিচাপে তলত দিয়া ধৰণে লিখিব পাৰিঃ

$\begin{array}{cc}𝐚& =\frac{d𝐯}{dt}\\ & =\frac{\mathrm{d}v}{\mathrm{d}t}{𝐮}_{\mathrm{t}}+v(t)\frac{d{𝐮}_{\mathrm{t}}}{dt}\\ & =\frac{\mathrm{d}v}{\mathrm{d}t}{𝐮}_{\mathrm{t}}+\frac{v^2}{R}{𝐮}_{\mathrm{n}},\\ \end{array}$

য’ত, u_n হৈছে পদাৰ্থ কণিকাটোৰ গতিপথৰ একক অভিলম্ব ভেক্টৰ (ভিতৰলৈ), আৰু R হৈছে তাৎক্ষণিক ভাঁজ ব্যাসাৰ্ধ যিবোৰ t সময়ত অস্কুলেটিঙ চাৰ্কলৰ পৰা লোৱা। এই অংশবোৰক স্পৰ্শকীয় ত্বৰণ আৰু ৰৈশিক ত্বৰণ নাইবা অপকেন্দ্ৰিক ত্বৰণ (চাওক বৄত্তীয় গতি আৰু অপকেন্দ্ৰিক বল) বুলি কোৱা হয়।

বিশেষ অৱস্থাসমূহ

সমত্বৰণ

কোনো গতিশীল বস্তুৰ বেগৰ পৰিৱৰ্তন যদি সমান সময় অন্তৰালত সমান হয় তেতিয়া সেই বস্তুৰ ত্বৰণক সমত্বৰণ বোলা হয়। মাধ্যাকৰ্ষণৰ প্ৰভাৱত মুক্তভাৱে তললৈ পৰি থকা বস্তু এটা সমত্বৰণৰ এটা সাধাৰণ উদাহৰণ, কোনো আন বাধাৰ অনুপস্থিতিত মুক্তভাৱে তললৈ পৰি থকা বস্তু এটাৰ ত্বৰণ কেৱল মাধ্যাকৰ্ষণ বলৰ ওপৰত নিৰ্ভৰশীল হয় (ইয়াক মাধ্যাকৰ্ষণিক ত্বৰণো বোলা হয়)। নিউটনৰ দ্বিতীয় সূত্ৰৰ মতে কোনো বস্তুৰ ওপৰত ক্ৰিয়া কৰা বল (F),

$𝐅=m𝐠$

সৰণ, প্ৰাৰম্ভিক বেগ, অন্তিম বেগ, সময় আৰু ত্বৰণৰ মাজৰ সম্পৰ্ক তলৰ সমীকৰণসমূহেৰে প্ৰকাশ কৰিব পাৰি:

$𝐯=𝐮+𝐚t$

$𝐬=𝐮t+\frac{1}{2}𝐚t^2=\frac{(𝐮+𝐯)t}{2}$

$|𝐯{|}^2=|𝐮{|}^2+2𝐚\cdot 𝐬$

য’ত

$𝐬$ = সৰণ

$𝐮$ = প্ৰাৰম্ভিক বেগ

$𝐯$ = অন্তিম বেগ

$𝐚$ = সমত্বৰণ

$t$ = সময়

প্ৰথম অৱস্থাত ত্বৰণ আৰু গতিৰ দিশ একে নোহোৱা সমত্বৰণেৰে গতি কৰা বস্তু এটাৰ গতিক দূটা ভাগত বিভক্ত কৰিব পৰা যায়। এটা উপাংশ (ভাগ) ৰ বেগ স্থিৰ হয় আৰু আনটোৰ বেগ ওপৰৰ সমীকৰণেৰে নিৰ্ণয় কৰিব পাৰি, গেলিলিউৱে দেখুওৱাই গৈছিল যে এনে ত্বৰণেৰে গতি কৰা বস্তুৰ গতিপথ উপবৃত্তীয় হয়।

বৃত্তীয় গতি

সুষম বৃত্তীয় গতি হৈছে সমদ্ৰুতিৰে কিন্তু দিশৰ পৰিৱৰ্তনেৰে গতি কৰাৰ বাবে কোনো বস্তুৱে লাভ কৰা ত্বৰণৰ ঊদাহৰণ। এই ক্ষেত্ৰত বস্তুটোৱে সমদ্ৰুতিৰে গতি কৰি থাকে যদিও প্ৰতি মুহূৰ্ততে ইয়াৰ দিশৰ পৰিৱৰ্তন হৈ থকাৰ বাবে ইয়াৰ বেগৰ পৰিৱৰ্তন হৈ থাকে, এই বেগৰ দিশ বৃত্তৰ স্পৰ্শকৰ দিশত হয়। এই ক্ষেত্ৰত ত্বৰণৰ দিশ বৃত্তটোৰ কেন্দ্ৰাভিমুখী হয় আৰু ইয়াৰ মান:

$a=\frac{v^2}{r}$ হয়

য’ত v হৈছে বস্তুটোৰ দ্ৰুতি. বস্তুটোৰ radial acceleration তাৰ কৌণিক বেগ $\omega$ৰ পৰা নিৰ্ভয় কৰিব পাৰি,

$𝐚=-{\omega }^2𝐫.$

গতিকে সুষম বৃত্তীয় গতিৰে গতি কৰা বস্তু এটাৰ ত্বৰণ সদায় কেন্দ্ৰাভিমুখী হয় অৰ্থাত ই অভিকেন্দ্ৰীক, এই ক্ষেত্ৰত বৃত্তৰ স্পৰ্শকৰ দিশত থকা বস্তুটোৰ ৰৈখিক ভৰবেগ বাবে হোৱা ভুৱা বল (চিউড’ বল)এ অপকেন্দ্ৰীক বলৰ ভূমিকা পালন কৰে আৰু বস্তুটোক বৃত্তীয় গতি প্ৰদান কৰে।

আপেক্ষিকতাৰ সৈতে সম্পৰ্ক

কোনোৱে মধ্যাকৰ্ষণৰ বাবে অনুভৱ কৰা বল আৰু ত্বৰণৰ বাবে পোৱা একেই, যিহেতু এই দূই বল একেই যদি আপুনি মধ্যাকৰ্ষণৰ প্ৰভাৱ অনুভৱ কৰিছে তেনেহ’লে আপুনি ত্বৰিত হৈ আছে, আইনষ্টাইনে ইয়াক সমতাৰ সূত্ৰ বুলি কৈ গৈছে, আইনষ্টাইনৰ মতে কেৱল মাত্ৰ সেইসকলহে (বা সেইবোৰ বস্তুহে) ত্বৰিত হৈ নাথাকে যাৰ ওপৰত কোনো বলৰ প্ৰভাৱ নাথাকে। "

লগতে চাওক

• কৌণিক ত্বৰণ
• মধ্যাকৰ্ষণিক ত্বৰণ
• গতিৰ সমীকৰণ
• নিঊটনৰ গতিৰ সমীকৰণ

বাহ্যিক সংযোগ

• ত্বৰণ মাপক সৰল ত্বৰণ একক পৰিৱৰ্তক
• Measurespeed.com - ত্বৰণ মাপক সাঁচ:Webarchive প্ৰাৰম্ভিক বেগ, অন্তিম বেগ আৰু সময়ৰ ভিত্তিৰ ত্বৰণ মাপক